The “retirement spending smile”

Retirement spending shown to decrease with age

We have written a lot about the pattern of retirement spending, with “Will spending remain constant in retirement?”, from 2013, and “How much do I need to retire, revisited?”, of only three months ago, being particularly relevant. The underlying theme of these articles is that we don’t believe our “Rule of 25”, the suggestion that you need investment wealth of at least 25 times your expected annual retirement spending to be highly confident of financing a 30 year retirement, is conservative or an unrealistic “rule of thumb response” to the “How much do I need to retire” question.

However, a recent article in “Forbes” magazine, titled “What is the ‘Retirement Spending Smile’?”, by Professor Wade Pfau, a prominent US academic specialising in the financial planning field, provides another potential challenge to the robustness of the “Rule of 25”. It examines US research on retirement spending, by David Blanchett [1], that suggests spending tends to decrease both at and during retirement at a real rate of about 1% p.a.

The “Rule of 25” is based on being able to maintain a constant, inflation adjusted retirement spending amount, over a 30-year period. On the face of it, Blanchett’s research showing retirement spending falls with age suggests that the “Rule of 25” may result in retirees being encouraged to save more than they actually need to.

This article examines Blanchett’s research (or, more correctly, Pfau’s interpretation of it) in more detail and asks, even if accepted without further question, what adjustment would we make to our “Rule of 25”. Cutting to the chase, despite the implied large spending falls by mid- retirement, our conclusion is not very much!

How does the “retirement spending smile” affect retirement wealth?

Blanchett’s research tends to support a common three-decade view of retirement, with the first described as the “go-go years”, the second as the “slow-go” years and the third as the “no-go” years. Typically, the first ten years of retirement tend to be much the same as pre-retirement in terms of activity. The second is slower, with both health and energy declining while in the third decade activity falls significantly.

In terms of discretionary retirement spending, Blanchett observed a steady decrease in spending rather than a constant rate. However, non-discretionary health costs tended to rise sharply in the later years of retirement and, at some stage, offset the fall in discretionary spending. The chart below, from Pfau’s article, shows the spending “retirement smile” pattern observed by Blanchett:

While the pattern varies with different housing spending levels, Pfau uses the research to calculate the typical “spending smile” for a retiree that begins retirement with spending of $100,000 p.a., as revealed in the chart below:

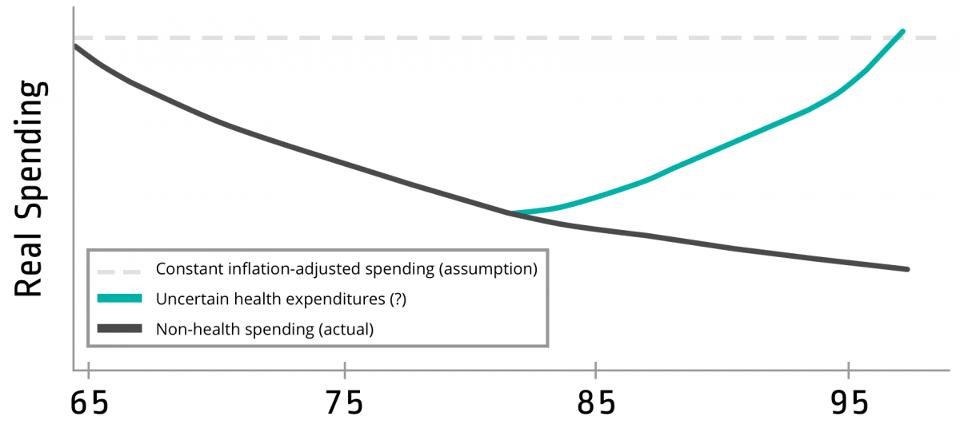
While the pattern varies with different housing spending levels, Pfau uses the research to calculate the typical “spending smile” for a retiree that begins retirement with spending of $100,000 p.a., as revealed in the chart below:

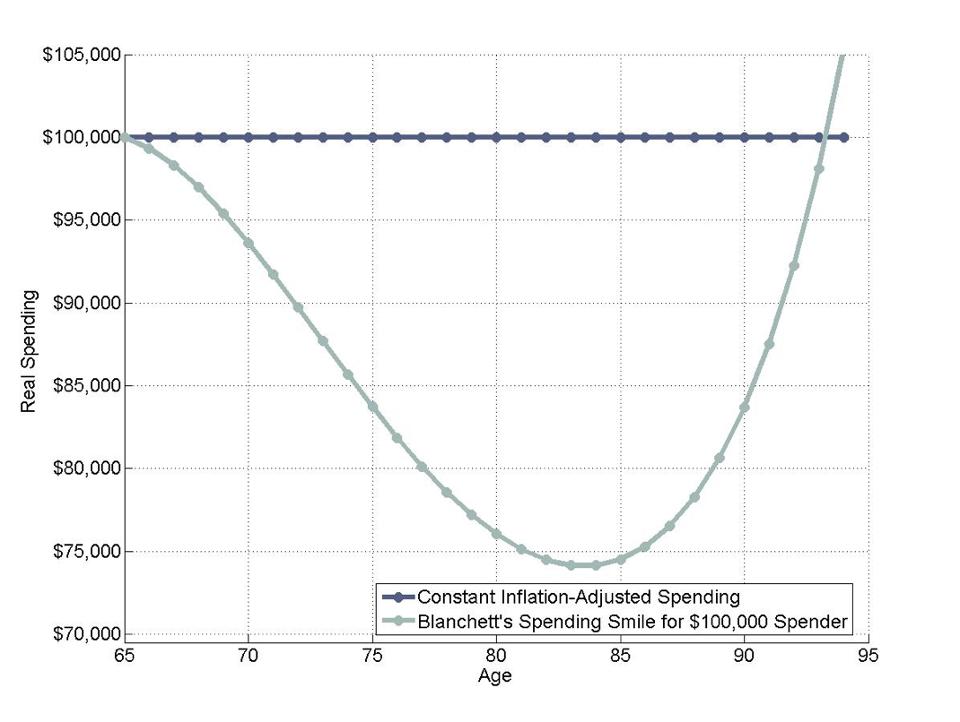
Spending falls to a little over $74,000 p.a. in real terms by age 84 and then rises with increases in health costs. Total spending over a 30-year retirement period is considerably less than the $3 million implied by a constant $100,000 p.a. spending assumption.

Now, while we have a number of reservations with the applicability of Blanchett’s research to our clients, what would it mean for the “Rule of 25” if we accepted the findings at face value i.e. all retirees will exhibit a retirement spending smile similar to that shown above. To assess this, we use a simulation technique called Monte Carlo and some reasonable, history based, investment assumptions [2] to first estimate the chances of running out of investment wealth over a 30-year retirement period commencing at age 65, assuming:

• Constant spending of $100,000 p.a.; and
• Initial wealth of $2.5 million i.e. 25 times desired spending.

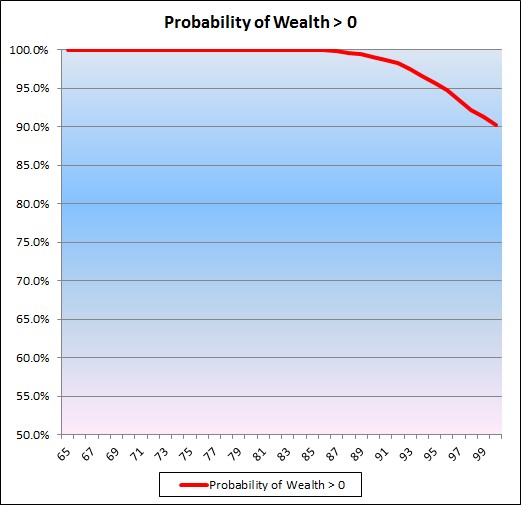
The chart below shows the calculated probability of investment wealth exceeding zero for ages 65 to 100. It indicates that the chance that wealth is positive at age 95 is 95.6% i.e. a 4.4% chance of consuming all investment wealth. This supports our claim that initial retirement wealth of 25 times desired constant annual spending provides a high probability of financing a 30-year retirement.

We then change the spending assumptions to approximately match the “spending smile” charted above, with the resulting probability of wealth greater than zero graph shown below:

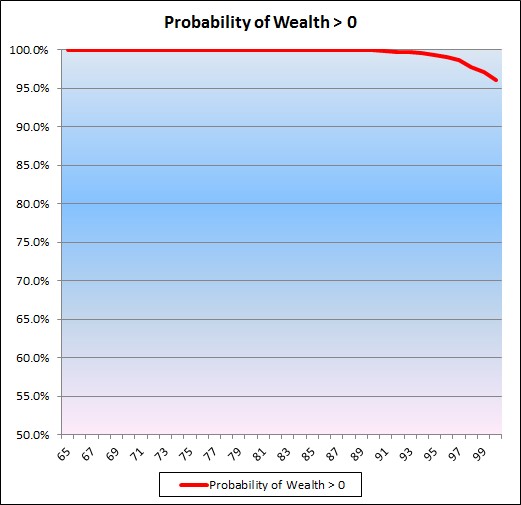
It reveals the probability of running out of investment wealth at age 95 is about 0.7%, considerably less than with constant spending. It also implies that an initial wealth requirement of 25 times desired initial annual spending may be too conservative.

We then investigated the probabilities of running out of investment wealth based on alternative multiples of initial spending, with the assumed “spending smile”. The results are tabled below:

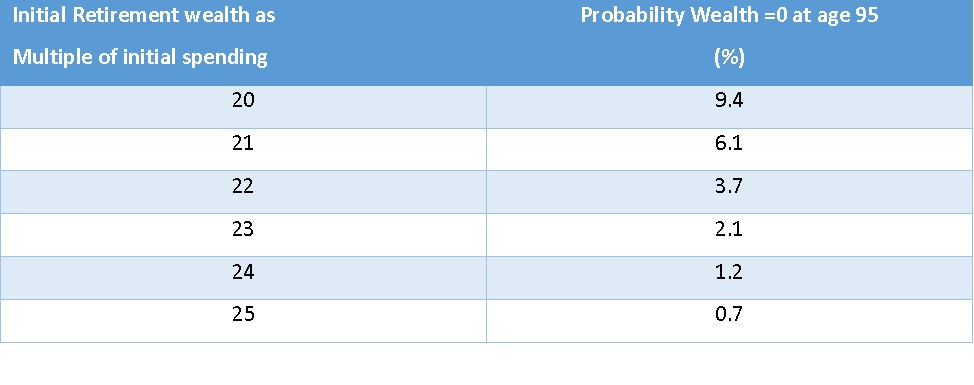
It indicates that a multiple of somewhere between 21 and 22, assuming a “retirement spending smile”, results in the same probability of running out of investment wealth as does a multiple of 25, based on constant annual spending (i.e. the 4.4% discussed above). Accepting the research without question therefore suggests a reduced initial wealth requirement of 12-16%, compared with that indicated by the “Rule of 25”.

The “retirement spending smile” offers little consolation

For most Australians nearing retirement, the possibility that they “only” need to accumulate 21-22 times their expected initial annual retirement spending, rather than 25, to be highly confident of funding a 30-year retirement will provide little consolation. It only reduces the size of the likely shortfall.

However, while Blanchett’s research is a valuable contribution to the retirement spending discussion, we stand by the final comment from our October 2016 article:

“The ‘Rule of 25’ provides a good starting point for discussion about the amount of initial wealth required that then may be modified depending on factors such as expectations regarding longevity, risk adjusted investment returns, investment risk tolerance, spending patterns and estate intentions.”

[1] David Blanchett, “Exploring the Retirement Consumption Puzzle”, Journal of Financial Planning, May 2014